Being a shamistician, rather than a statistician, I’m not sure how much importance to attach to this, but I thought it was interesting enough to share!
The JISC Library Impact Data Project has given us an opportunity to churn through our usage data again and, following on from the last blog post, we’ve been looking at the statistical significance (if any!) of the correlations we’re finding in the data.
The book loan data for the last 5 years of undergrads (who graduated with a specific honour) has a small overall Pearson correlation of -0.17 (see this blog post for an explanation of why it’s negative) with a high statistical significance (p-value of 0). However, when we looked at just the 2009/10 data (which is the period the other project partners are providing data for), we found a stronger correlation (-0.20).
If we go a step further and look at the Pearson correlation each year, there appears to be a possible underlying trend at Huddersfield…
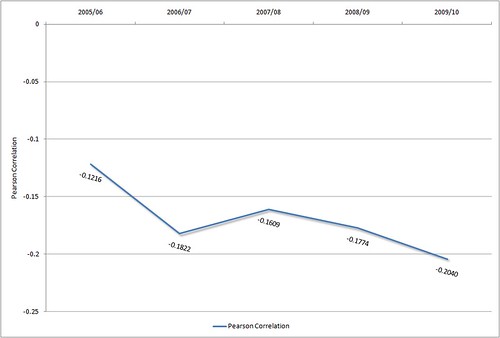
If you accept that there might be a trend there (with the Pearson correlation value increasing over time), then it raises an interesting question… are books becoming an increasingly more important part of achieving a higher grade?
4 thoughts on “Are books becoming more important?”
Comments are closed.
Just as an aside, we’re just talking about physical loans here — ebook usage data isn’t included.
that’s what the graph seems to point to, but at the same time, moving from 0.12 to 0.20… it’s still a very weak correlation, is it not? What would be considered a good correlation?
Totally agree it’s a weak correlation (altho the p-value is very close to 0 for every year, so the weak correlation is still statistically significant).
From what I understand of Pearson, the correlation value is affected by outliers and we’re seeing sizeable minorities of non & low usage for each grade. I’m not sure how much of an affect that has on the value?
From the other data we’ve received so far (2 other libraries), their loan & grade correlation is of a similar value (-0.163 and -0.178). Once we get the other 5 sets of data in, I’ll post their correlation values.
One has to be a big careful testing lots of things for ‘statistical significance’, and figuring when you find some relationship the equation says is ‘significant’. The probability calculations behind those equations are based on assumptions that you make a hypothesis, do an experiment, and then see if it came out how you thought. If you instead take some data without a hypothesis in advance, and examine every single possible relationship between two variables you can think of — surely some of them will come up as appearing corelated just coincidentally by chance.
For instance, imagine getting 100k pennies from the bank and flipping them each 100 times — you could calculate how likely it is that at least one of them will be heads all 100 times, but that calculation is going to be based on you having 100k pennies. Testing dozens or hundreds of things in your data for ‘significance’ and then figuring the one that comes up significant is — is like using a calculation for the likelyhood that penny flipped 100x will come up heads all 100x times just by chance — but then doing it with hundreds of pennies, and then when you get one that flips heads 100x, deciding it couldn’t have done that just by chance. If you just had one penny, it’d be awfully unlikely, sure, but it’s more likely that at least ONE of those pennies will flip heads 100 times when you start with 100k of them!
But don’t get me wrong, a large portion of published research in general is based on just this kind of bad statistics. But it’s still bad statistics. I think there’s a well-cited article somewhere on ‘why most published research is wrong’ or something like that, that mentions this mis-use of statistics as one factor.